Consistent Hashing

#Golang #distributed

在前面 Redis和Memcached区别中介绍过， Memcached 的分布式是通过客户端的一致性哈希算法实现的，在ARTS-WEEK10中，分享了一致性hash算法，现在来具体看看。

一致性哈希算法在1997年由Karger等人在解决分布式Cache问题时提出。在CDN系统、分布式hash表、消息中间件、分布式缓存中有着广泛的应用。

一致性哈希算法原理

假设存在N台缓存服务器，要把数据均匀的分布在这N台缓存中，最基本的做法莫过于hash取模，即将key值为K的数据路由到hash(K) mod N对应的机器。只要key值具有一定随机性，数据就能达到很好的负载均衡。但是这种结构，在分布式系统中就不适用了。分布式系统中的每个节点都有失效的可能，并且新的节点很可能动态增加进来。继续使用Hash取模的方法，影响是灾难性的，每次有节点增加或删除，旧有的数据分布大量失效。因此一致性哈希就显得至关重要了。

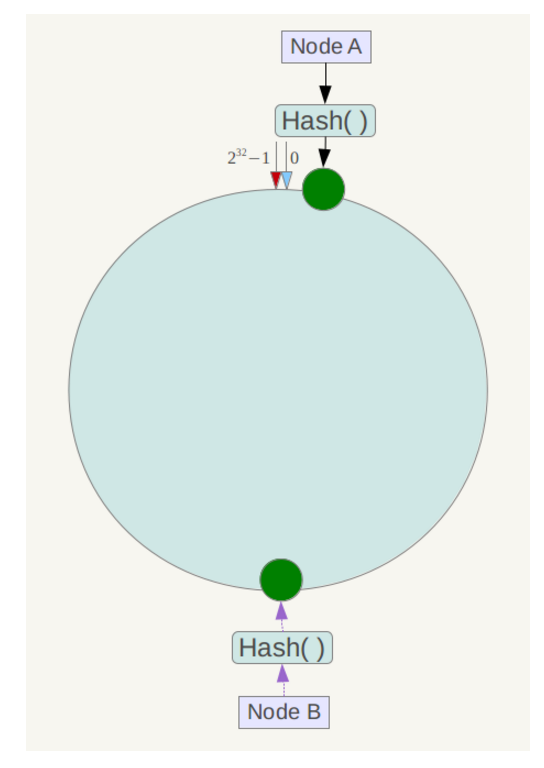
一致性哈希算法（Consistent Hashing）最早在论文《Consistent Hashing and Random Trees: Distributed Caching Protocols for Relieving Hot Spots on the World Wide Web》中被提出。简单来说，一致性哈希将整个哈希值空间组织成一个虚拟的圆环，如假设某哈希函数H的值空间为0-2^32-1（即哈希值是一个32位无符号整形），整个哈希空间环如下：

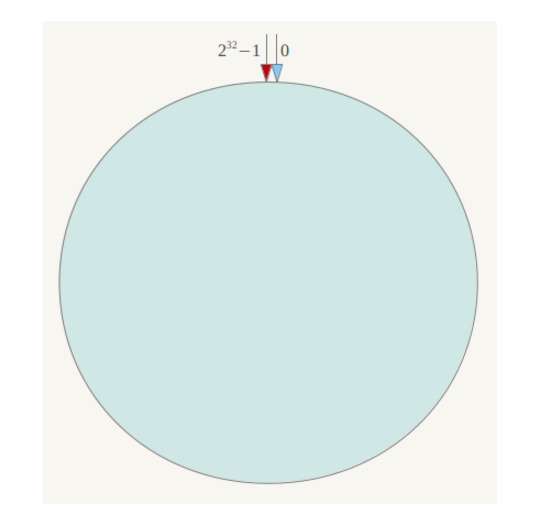
整个空间按顺时针方向组织，0和2^32-1在零点重合。

下一步计算服务器的hash值，可以选定服务器的IP或主机名作为关键字进行哈希，这样服务器就分布在这个哈希空间环上：

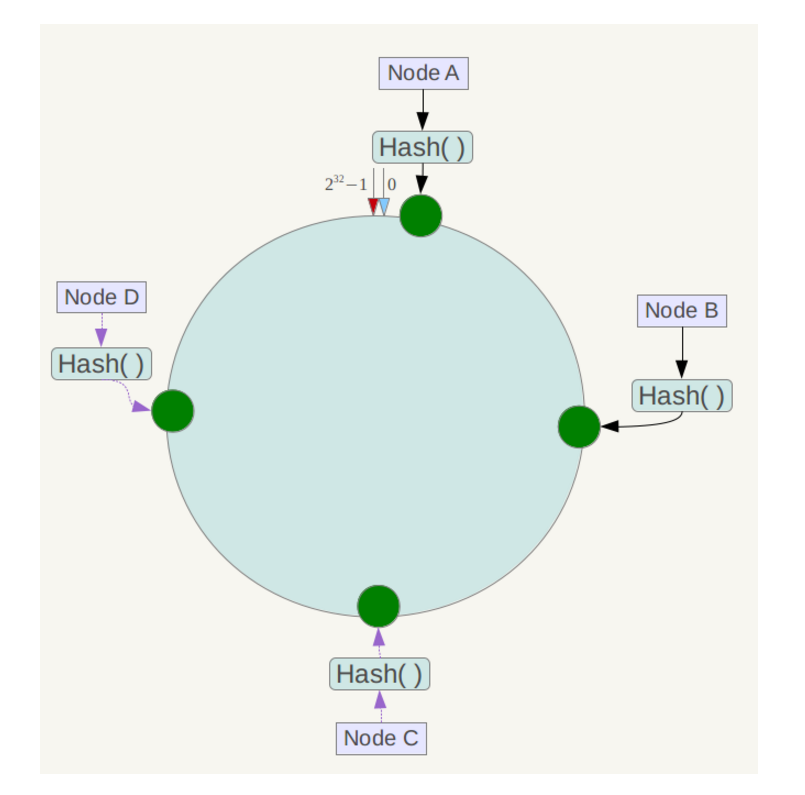
接下来使用如下算法定位数据访问到相应服务器：将数据key使用相同的函数Hash计算出哈希值，并确定此数据在环上的位置，将其定位到顺时针方向遇到的第一台服务器上。

假设有Object A、Object B、Object C、Object D四个数据对象，经过哈希计算后，在环空间上的位置如下：

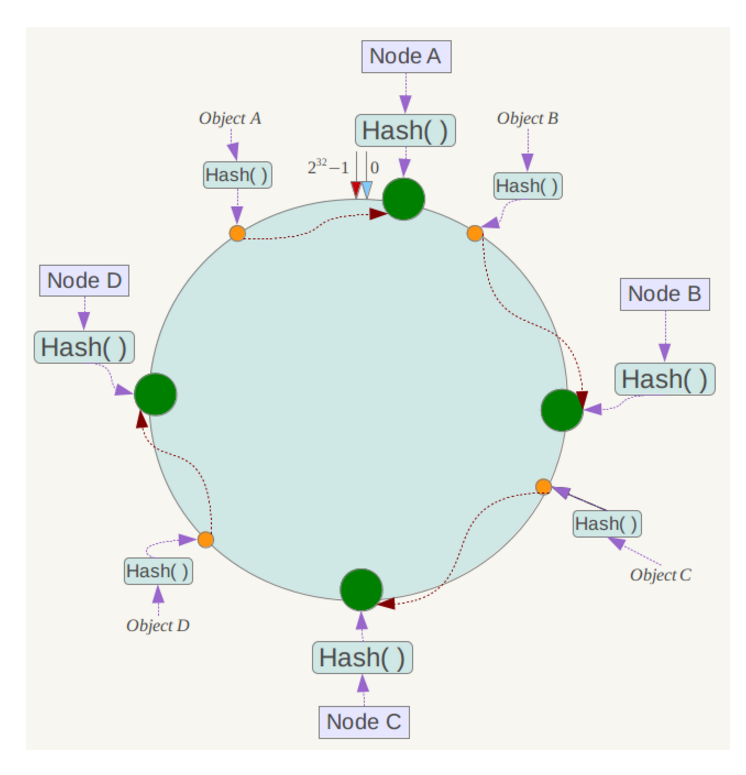
根据一致性哈希算法，数据A会被定为到Node A上，B被定为到Node B上，C被定为到Node C上，D被定为到Node D上。

以上就是一致性哈希的处理过程，现在分析下一致性哈希的容错性和可扩展性。假设Node C不幸宕机，可以看到此时对象A、B、D不会受到影响，只有C对象被重定位到Node D。一般的，在一致性哈希算法中，如果一台服务器不可用，则受影响的数据仅仅是此服务器到其环空间中前一台服务器（即沿着逆时针方向行走遇到的第一台服务器）之间数据，其它不会受到影响。

另一种情况，在系统中增加一台服务器Node X，如下图所示：

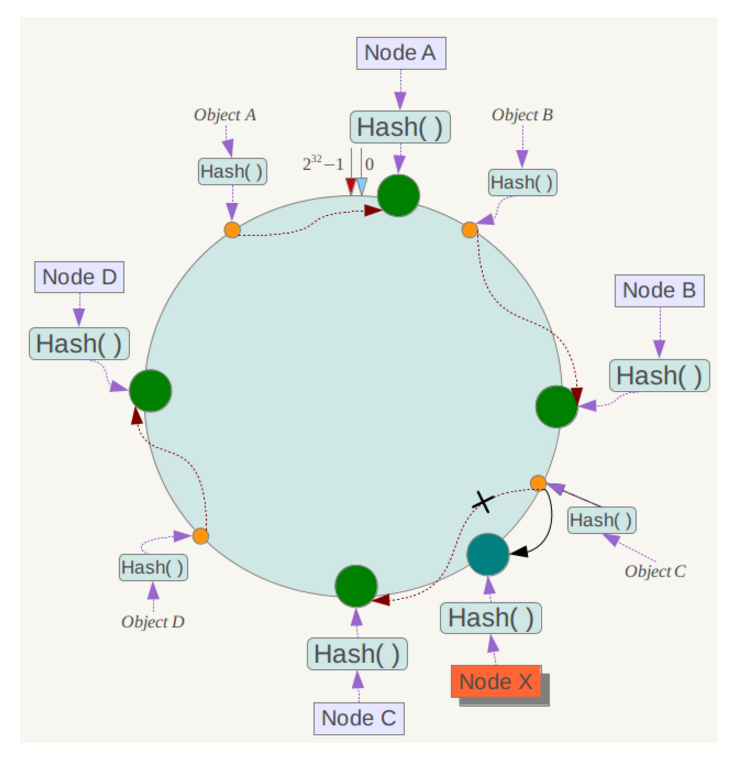
此时对象Object A、B、D不受影响，只有对象C需要重定位到新的Node X 。一般的，在一致性哈希算法中，如果增加一台服务器，则受影响的数据仅仅是新服务器到其环空间中前一台服务器（即沿着逆时针方向行走遇到的第一台服务器）之间数据，其它数据也不会受到影响。

综上，一致性哈希算法对于节点的增减都只需重定位环空间中的一小部分数据，具有较好的容错性和可扩展性。

另外，一致性哈希在节点较少时可能存在数据倾斜的问题，即如下图的情况下，系统中只有两台服务器，大量的数据集中在Node A上，只有极少的定位到Node B上。

为此，一致性哈希算法引入了虚拟节点机制，即对每一台服务器计算多个哈希。具体做法是在服务器的ip或者主机名后面加上编号，比如Node A，可以计算“Node A|1”，“Node A|2”，“Node A|3”，这样两个节点就变成了6个节点，放入虚拟节点“Node A|2”的数据实际放入了Node A中。在实际应用中，通常将虚拟节点数设置为32甚至更大，因此即使很少的服务节点也能做到相对均匀的数据分布。

一致性哈希算法实现

Consistent hashing的维基百科中，给出了各种语言的实现方式链接，这里主要介绍以下Go的版本，其他语言版本的实现类似，Go使用CRC-32-IEEE 802.3作为hash函数，python版和java版使用md5作为hash函数。

完整代码见：

https://github.com/stathat/consistent

// Consistent存放哈希环上的节点信息
// circle存放虚拟节点与真实节点的对应关系
// members存放真实节点的信息
// sortedHashes存放排序(升序)后的hash值
// NumberOfReplicas为虚拟节点数，初始化为20
// count真实节点个数
type Consistent struct {
	circle           map[uint32]string
	members          map[string]bool
	sortedHashes     uints
	NumberOfReplicas int
	count            int64
	scratch          [64]byte
	sync.RWMutex
}

func New() *Consistent {
	c := new(Consistent)
	c.NumberOfReplicas = 20
	c.circle = make(map[uint32]string)
	c.members = make(map[string]bool)
	return c
}

新增节点的过程：

func (c *Consistent) Add(elt string) {
	c.Lock()
	defer c.Unlock()
	c.add(elt)
}

func (c *Consistent) add(elt string) {
	for i := 0; i < c.NumberOfReplicas; i++ {
		c.circle[c.hashKey(c.eltKey(elt, i))] = elt
	}
	c.members[elt] = true
	c.updateSortedHashes()
	c.count++
}

func (c *Consistent) eltKey(elt string, idx int) string {
	// return elt + "|" + strconv.Itoa(idx)
	return strconv.Itoa(idx) + elt
}

func (c *Consistent) updateSortedHashes() {
	hashes := c.sortedHashes[:0]
	//reallocate if we're holding on to too much (1/4th)
	if cap(c.sortedHashes)/(c.NumberOfReplicas*4) > len(c.circle) {
		hashes = nil
	}
	for k := range c.circle {
		hashes = append(hashes, k)
	}
	sort.Sort(hashes)
	c.sortedHashes = hashes
}

新增节点的过程主要包含两步：

计算虚拟节点的hash
更新hash值得顺序(updateSortedHashes)

删除节点的过程类似：

func (c *Consistent) Remove(elt string) {
	c.Lock()
	defer c.Unlock()
	c.remove(elt)
}


func (c *Consistent) remove(elt string) {
	for i := 0; i < c.NumberOfReplicas; i++ {
		delete(c.circle, c.hashKey(c.eltKey(elt, i)))
	}
	delete(c.members, elt)
	c.updateSortedHashes()
	c.count--
}

可以调用Get方法定位数据访问到相应服务器：

func (c *Consistent) Get(name string) (string, error) {
	c.RLock()
	defer c.RUnlock()
	if len(c.circle) == 0 {
		return "", ErrEmptyCircle
	}
	key := c.hashKey(name)
	i := c.search(key)
	return c.circle[c.sortedHashes[i]], nil
}

func (c *Consistent) search(key uint32) (i int) {
	f := func(x int) bool {
		return c.sortedHashes[x] > key
	}
	i = sort.Search(len(c.sortedHashes), f)
	if i >= len(c.sortedHashes) {
		i = 0
	}
	return
}

定位的方法主要有三步：

计算数据的hash值
通过search方法获取顺时针方向第一个节点的hash值
通过节点的hash值，得到对应的节点

使用的hash算法：

func (c *Consistent) hashKey(key string) uint32 {
	if len(key) < 64 {
		var scratch [64]byte
		copy(scratch[:], key)
		return crc32.ChecksumIEEE(scratch[:len(key)])
	}
	return crc32.ChecksumIEEE([]byte(key))
}

通过循环冗余校验计算出key值得32位整数，即相当于映射到0-2^32-1的哈希环上。

参考：

https://www.cnblogs.com/lpfuture/p/5796398.html

https://en.m.wikipedia.org/wiki/Consistent_hashing

https://github.com/stathat/consistent

https://leileiluoluo.com/posts/consistent-hashing-and-high-available-cluster-proxy.html

https://zh.wikipedia.org/wiki/%E5%BE%AA%E7%92%B0%E5%86%97%E9%A4%98%E6%A0%A1%E9%A9%97